Follow Duniaku untuk mendapatkan informasi terkini. Klik untuk follow WhatsApp Channel & Google News
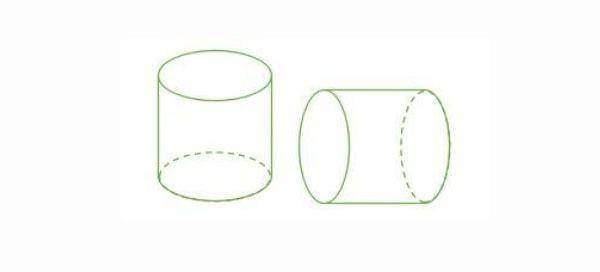
Tabung adalah sebuah ruang yang mempunyai sisi lengkung dengan susunan tutup dan alas berukuran sama dan sejajar yang berbentuk lingkaran, kemudian bagian sisi lengkung diselimuti dengan persegi panjang. Kalian bisa menemukan tabung di kehidupan sehari-hari, seperti drum, kayu yang telah dipotong, pipa, bambu, dan lain lain.
Tabung adalah bangun ruang yang memiliki volume. Dalam pembahasan ini, duniaku.com akan menjelaskan mengenai tabung yang meliputi pengertian, ciri-ciri, unsur, rumus volume, dan contoh soal.
1. Pengertian tabung
Tabung merupakan sebuah bangun ruang tiga dimensi dengan bagian alas dan tutup yang mempunyai ukuran sama, serta terdapat selimut berbentuk persegi panjang yang mengelilingi kedua lingkaran.
Contoh nyata dari bentuk tabung adalah botol minum, termos, atau kaleng makanan yang berbentuk tabung.
2. Ciri-ciri tabung
Terdapat beberapa ciri khas dari tabung yang membedakan dengan bentuk lainnya. Berikut ini ciri-ciri tabung yang perlu diketahui.
- Tabung terdiri dari 2 buah rusuk.
- Tabung mempunyai alas dan atap yang berbentuk lingkaran dengan ukuran yang sama.
- Terdapat 3 sisi pada tabung, yakni bagian alas, tutup, dan selimut.
3. Unsur-unsur tabung
Setelah mengetahui ciri-ciri tabung, berikutnya terdapat unsur-unsur dari terbentuknya sebuah tabung. Berikut ini unsur-unsur tabung yang perlu diketahui.
- Sisi tabung: suatu bidang yang membentuk tabung dengan dua buah lingkaran di bagian atap dan bagian alas serta sebuah selimut.
- Selimut tabung: sebuah bidang yang menutupi bagian tertenu pada bentuk tabung. Selimut tabung memiliki bentuk persegi panjang.
- Diameter: ketika suatu tabung dipotong di bagian tengah menjadi ukuran yang sama, maka jarak potongan disebut sebagai diameter tabung tersebut.
- Jari-jari: setengah dari diameter suatu tabung.
4. Rumus volume tabung
Dalam menyelesaikan soal Matematika yang berkaitan dengan tabung, biasanya kita akan diharuskan mencari hasil volume, keliling, dan luas permukaan sebuah tabung. Berikut ini terdapat rumus tabung yang perlu kalian ketahui.
Rumus Volume Tabung
V = π x r x r x t
Keterangan:
V = volume tabung (m3)
π = phi (3,14 atau 22/7)
r = tinggi tabung (m)
t = tinggi tabung (m)
Rumus Keliling Tabung
K = π x d
Keterangan:
K = Keliling alas atau tutup
π = Phi (22/7 atau 3,14)
d = diameter
Rumus Luas Permukaan Tabung
Alas atau tutup = π x r2
Selimut = K x t
Atau, Luas permukaan = (2 x luas alas) + luas selimut
Keterangan:
K = Keliling alas atau tutup
π = phi (22/7 atau 3,14)
r = jari-jari
t = tinggi tabung
5. Contoh soal 1
Jika ingin memahami cara menyelesaikan soal yang berkaitan dengan volume, keliling alas, dan luas permukaan tabung, kalian perlu mencoba contoh soal tabung dan memasukkan rumus yang telah disebutkan untuk mendapatkan hasil yang benar. Berikut ini terdapat beberapa contoh soal tabung.
- Diketahui:
Bapak memiliki sebuah tabung yang memiliki diameter 14 cm dan tinggi tabung sekitar 10 cm.
- Pertanyaan:
Berapa keliling alas, luas permukaan, volume tabung dari contoh di atas?
- Jawaban:
Diketahui tabung memiliki diameter 14 cm, sehingga jari-jarinya adalah 7 cm.
Keliling Alas Tabung
K = π x d
= 22/7 x 14
= 44 cm
Luas Permukaan Tabung
Luas alas = π x r2
= 22/7 x 72
= 154 cm2
Luas selimut = K x t
= 44 x 10
= 440 cm2
Luas permukaan tabung = (2 x luas alas) + luas selimut
= (2 x 154) + 440
= 308 + 440
= 748 cm2
Volume Tabung
Volume = luas alas x t
= 154 x 10
= 1540 cm3
Setelah perhitungan menggunakan rumus, maka jawaban dari pertanyaannya adalah sebagai berikut.
- Keliling alas tabung adalah 44 cm.
- Luas permukaan tabung adalah 748 cm2.
- Volume tabung adalah 1540 cm3.
6. Contoh soal 2
Semakin banyak latihan soal, tentu akan semakin meningkatkan pemahaman kalian terhadap rumus matematika. Nah, mari kita coba contoh soal yang kedua.
- Diketahui:
Terdapat seorang anak yang memiliki sebuah tabung dengan jari-jari sepanjang 7 cm dan tinggi tabung sekitar 30 cm.
r = 7 cm
t = 30 cm
- Pertanyaan:
Tentukan volume air dari tabung tersebut dengan menggunakan rumus yang tepat.
- Jawaban:
Volume Tabung = π x r2 x t
= 22/7 x 72 x 30 cm
= 22/7 x 49 30 cm
= 4.620 cm3
Jadi, volume air tabung adalah 4.620 cm3.
Demikian ulasan mengenai tabung yang meliputi pengertian, ciri-ciri, unsur-unsur, rumus, hingga contoh soal yang dapat membantu kalian dalam memahami persoalan matematika yang berkaitan dengan tabung. Berdasarkan ulasan di atas, bagaimana menurut kalian mengenai bangun ruang tabung?
Diterbitkan pertama 22 Desember 2022, diterbitkan kembali 15 November 2024.
Baca Juga: Rumus Volume Kerucut Lengkap dengan Contoh Soal dan Jawabannya
Baca Juga: Rumus Volume Prisma Segitiga, Lengkap dengan Contoh Soal!
Baca Juga: Rumus Volume Limas Segi Empat (dengan Contoh Soal dan Jawaban)